钦定古今图书集成经济汇编乐律典
第六十二卷目录
律吕部汇考十六
明朱载堉律吕精义二〈不取围径皆同〉
明朱载堉律吕精义二〈不取围径皆同〉
乐律典第六十二卷
律吕部汇考十六
明·朱载堉《律吕精义二》不取围径皆同第五之上旧律围径皆同,而新律各不同。《礼记注疏》曰:凡律,空围九分。《月令章句》曰:围数无增减。及《隋志》安丰王等说,皆不足取也。故著此论。论曰:琴瑟不独徽柱之有远近,而弦亦有巨细焉。笙竽不独管孔之有高低,而簧亦有厚薄焉。弦之巨细若一,但以徽柱远近别之,不可也。簧之厚薄若一,但以管孔高低别之,不可也。譬诸律管,虽有修短之不齐,亦有广狭之不等。先儒以为长短虽异,围径皆同,此未达之论也。今若不信,以竹或笔管制黄钟之律,一样二枚,截其一枚分作两段,全律、半律,各令一人吹之,声必不相合矣。此昭然可验也。又制大吕之律,一样二枚,周径与黄钟同,截其一枚分作两段,全律、半律,各令一人吹之,则亦不相合。而大吕半律乃与黄钟全律相合,略差不远。是知所谓半律者,皆下全律一律矣。大抵管长则气隘,隘则虽长而反清。管短则气宽,宽则虽短而反浊。此自然之理,先儒未达也。要之长短广狭,皆有一定之理,一定之数在焉。置黄钟倍律九而一,以为外周,用弦求句股术,得其内周,又置倍律四十而一以为内径,用句股求弦术得其外径,盖律管两端形如环田,有内外周径焉。外周内容之方,即内径也。内周外射之斜,即外径也。方圆相容,天地之象,理数之妙者也。黄钟通长八十一分者,内周九分,是为八十一中之九,即约分法九分中之一也。若约黄钟八十一分,作为九寸,则其内周当云一寸,旧以九十分为黄钟,而云空围九分者,误也。况又穿凿指为面,羃九方分,则误益甚矣。方圆相容,有图如左。
密率周径图密率周径图
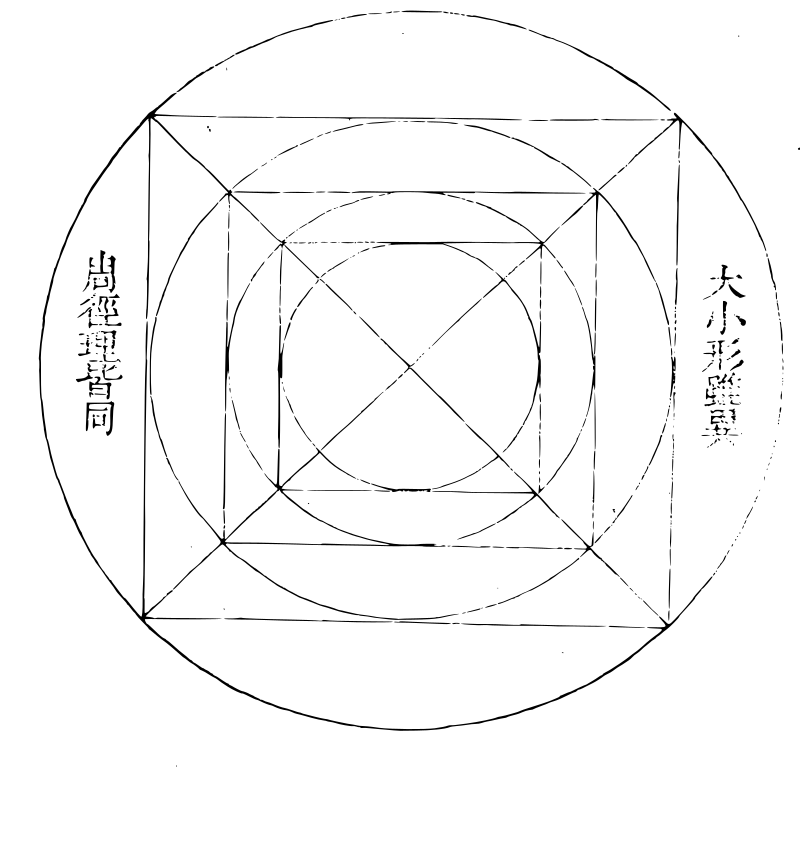
第一层,倍
律外周也。
第二层,倍
律内周,即
正律外周
也。三层、四
层皆放此
推之。
密率源流图密率源流图
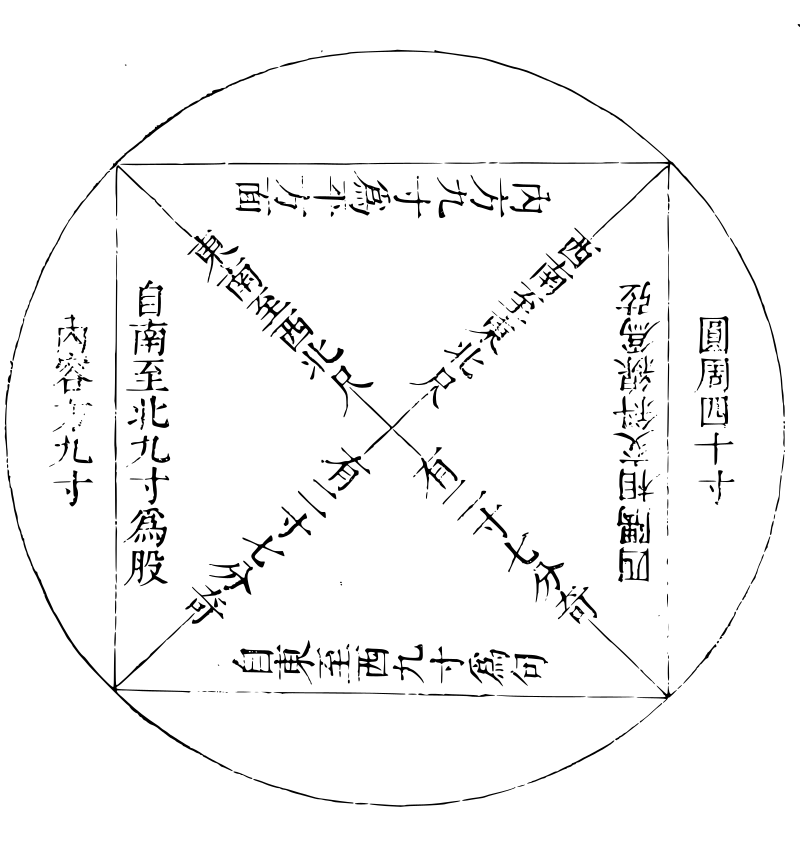
法曰:圆周
四十容方
九,句股求
弦数,可知,
遂以此为
求径率。求
周求积,亦
如之。
新法密率算术,周径羃积相求。
周求径者,置周全数九,因四十除之,所得自乘倍之为实。开平方法除之,得径,径求周者,置径全数,自乘半之为实。开平方法除之,所得四十,乘之九,归得周。周求积者,置周全数九,因四十除之,所得自乘倍之为实。径求积者,置径全数自乘为实。二项各又自乘,以一百乘之,一百六十二除之,所得为实。开平方法除之,得积,积求周径者,置积全数自乘,所得以一百六十二乘之,一百除之,为实。开平方法除之,所得副置之其一,折半为实。开平方法除之,所得四十,乘之九,归得周,其一不须折半,但以开平方法除之,得径。所谓积者,面羃平圆积也。以其通长乘之,各得其实积也。
旧法,平圆周径积,互相求,但系围三径一术者,皆疏舛不可用。惟周径相乘,四归得积,及半周、半径相乘,得积,二者可用。
先求三十六律通长真数。
黄钟倍律通长二尺,容黍二合,称重二两。律度量
衡无非倍者,此自然全数也。故算法皆从倍律起,若夫正律于度虽足,于量于衡,则皆不足,祇容半合,祇重半两,比诸倍律似非自然全数,故算法不从正律起,亦不从半律起。倍律、正律、半律,各有十二,共为三十六律。
置黄钟倍律通长二尺为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺八寸八分七釐七毫四丝八忽六微二纤,为大吕。置大吕倍律通长一尺八寸八分七釐七毫四丝八忽六微二纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺七寸八分一釐九毫九丝七忽四微三纤,为太蔟。置太蔟倍律通长一尺七寸八分一釐七毫九丝七忽四微三纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺六寸八分一釐七毫九丝二忽八微三纤,为夹钟。置夹钟倍律通长一尺六寸八分一釐七毫九丝二忽八微三纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺五寸八分七釐四毫○一忽○五纤,为姑洗。置姑洗倍律通长一尺五寸八分七釐四毫○一忽○五纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺四寸九分八釐三毫○七忽○七纤,为仲吕。置仲吕倍律通长一尺四寸九分八釐三毫○七忽○七纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺四寸一分四釐二毫一丝三忽五微六纤,为蕤宾。置蕤宾倍律通长一尺四寸一分四釐二毫一丝三忽五微六纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺三寸三分四釐八毫三丝九忽八微五纤,为林钟。置林钟倍律通长一尺三寸三分四釐八毫三丝九忽八微五纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺二寸五分九釐九毫二丝一忽○四纤,为夷则。置夷则倍律通长一尺二寸五分九釐九毫二丝一忽○四纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺一寸八分九釐二毫○七忽一微一纤,为南吕。置南吕倍律通长一尺一寸八分九釐二毫○七忽一微一纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺一寸二分二釐四毫六丝二忽○四纤,为无射。置无射倍律通长一尺一寸二分二釐四毫六丝二忽○四纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺○五分九釐四毫六丝三忽○九纤,为应钟。置应钟倍律通长一尺○五分九釐四毫六丝三忽○九纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得一尺,为黄钟。
置黄钟正律通长一尺为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得九寸四分三釐八毫七丝四忽三微一纤,为大吕。置大吕正律通长九寸四分三釐八毫七丝四忽三微一纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得八寸九分○八毫九丝八忽七微一纤,为太蔟。置太蔟正律通长八寸九分○八毫九丝八忽七微一纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得八寸四分○八毫九丝六忽四微一纤,为夹钟。置夹钟正律通长八寸四分○八毫九丝六忽四微一纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得七寸九分三釐七毫○○五微二纤,为姑洗。置姑洗正律通长七寸九分三釐七毫○○五微二纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得七寸四分九釐一毫五丝三忽五微三纤,为仲吕。置仲吕正律通长七寸四分九釐一毫五丝三忽五微三纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得七寸○七釐一毫○六忽七微八纤,为蕤宾。置蕤宾正律通长七寸○七釐一毫○六忽七微八纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得六寸六分七釐四毫一丝九忽九微二纤,为林钟。置林钟正律通长六寸六分七釐四毫一丝九忽九微二纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得六寸二分九釐九毫六丝○五微二纤,为夷则。置夷则正律通长六寸二分九釐九毫六丝○五微二纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得五寸九分四釐六毫○三忽五微五纤,为南吕。置南吕正律通长五寸九分四釐六毫○三忽五微五纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得五寸六分一釐二毫三丝一忽○二纤,为无射。置无射正律通长五寸六分一釐二毫三丝一忽○二纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得五寸二分九釐七毫三丝一忽五微四纤,为应钟。置应钟正律通长五寸二分九釐七毫三丝一忽五微四纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得五寸,为黄钟。
置黄钟半律通长五寸为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得四寸七分一釐九毫三丝七忽一微五纤,为大吕。置大吕半律通长四寸七分一釐九毫三丝七忽一微五纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得四寸四分五釐四毫四丝九忽三微五纤,为太蔟。置太蔟半律通长四寸四分五釐四毫四丝九忽三微五纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得四寸二分○四毫四丝八忽二微○,为夹钟。
置夹钟半律通长四寸二分○四毫四丝八忽二微○为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得三寸九分六釐八毫五丝○二微六纤,为姑洗。置姑洗半律通长三寸九分六釐八毫五丝○二微六纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得三寸七分四釐五毫七丝六忽七微六纤,为仲吕。置仲吕半律通长三寸七分四釐五毫七丝六忽七微六纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得三寸五分三釐五毫五丝三忽三微九纤,为蕤宾。置蕤宾半律通长三寸五分三釐五毫五丝三忽三微九纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得三寸三分三釐七毫○九忽九微六纤,为林钟。置林钟半律通长三寸三分三釐七毫○九忽九微六纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得三寸一分四釐九毫八丝○二微六纤,为夷则。置夷则半律通长三寸一分四釐九毫八丝○二微六纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得二寸九分七釐三毫○一忽七微七纤,为南吕。置南吕半律通长二寸九分七釐三毫○一忽七微七纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得二寸八分○六毫一丝五忽五微一纤,为无射。置无射半律通长二寸八分○六毫一丝五忽五微一纤为实,以十亿乘之,以十亿○五千九百四十六万三千○九十四除之,得二寸六分四釐八毫六丝五忽七微七纤,为应钟。次求三十六律外周真数。
先置黄钟倍律通长二尺为实,九归得二寸二分二釐二毫二丝二忽二微二纤,为其外周。就置所得为实,依后项乘除之。
置黄钟倍律外周二寸二分二釐二毫二丝二忽二微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二寸一分五釐八毫九丝五忽九微八纤,为大吕。置大吕倍律外周二寸一分五釐八毫九丝五忽九微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二寸○九釐七毫四丝九忽八微四纤,为太蔟。置太蔟倍律外周二寸○九釐七毫四丝九忽八微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二寸○三釐七毫七丝八忽六微七纤,为夹钟。置夹钟倍律外周二寸○三釐七毫七丝八忽六微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸九分七釐九毫七丝七忽四微九纤,为姑洗。置姑洗倍律外周一寸九分七釐九毫七丝七忽四微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸九分二釐三毫四丝一忽四微五纤,为仲吕。置仲吕倍律外周一寸九分二釐三毫四丝一忽四微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸八分六釐八毫六丝五忽八微七纤,为蕤宾。置蕤宾倍律外周一寸八分六釐八毫六丝五忽八微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸八分一釐五毫四丝六忽一微六纤,为林钟。置林钟倍律外周一寸八分一釐五毫四丝六忽一微六纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸七分六釐三毫七丝七忽八微九纤,为夷则。置夷则倍律外周一寸七分六釐三毫七丝七忽八微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸七分一釐三毫五丝六忽七微五纤,为南吕。置南吕倍律外周一寸七分一釐三毫五丝六忽七微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸六分六釐四毫七丝八忽五微六纤,为无射。置无射倍律外周一寸六分六釐四毫七丝八忽五微六纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸六分一釐七毫三丝九忽二微四纤,为应钟。置应钟倍律外周一寸六分一釐七毫三丝九忽二微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸五分七釐一毫三丝四忽八微四纤,为黄钟。置黄钟正律外周一寸五分七釐一毫三丝四忽八微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸五分二釐六毫六丝一忽五微一纤,为大吕。置大吕正律外周一寸五分二釐六毫六丝一忽五微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸四分八釐三毫一丝五忽五微三纤,为太蔟。置太蔟正律外周一寸四分八釐三毫一丝五忽五微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸四分四釐○九丝三忽二微八纤,为夹钟。置夹钟正律外周一寸四分四釐○九丝三忽二微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸三分九釐九毫九丝一忽二微二纤,为姑洗。置姑洗正律外周一寸三分九釐九毫九丝一忽二微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸三分六釐○○五忽九微四纤,为仲吕。置仲吕正律外周一寸三分六釐○○五忽九微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸三分二釐一毫三丝四忽一微二纤,为蕤宾。置蕤宾正律外周一寸三分二釐一毫三丝四忽一微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸二分八釐三毫七丝二忽五微二纤,为林钟。置林钟正律外周一寸二分八釐三毫七丝二忽五微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸二分四釐七毫一丝八忽○○,为夷则。
置夷则正律外周一寸二分四釐七毫一丝八忽○○为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸二分一釐一毫六丝七忽五微二纤,为南吕。置南吕正律外周一寸二分一釐一毫六丝七忽五微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸一分七釐七毫一丝八忽一微二纤,为无射。置无射正律外周一寸一分七釐七毫一丝八忽一微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸一分四釐三毫六丝六忽九微一纤,为应钟。置应钟正律外周一寸一分四釐三毫六丝六忽九微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸一分一釐一毫一丝一忽一微一纤,为黄钟。置黄钟半律外周一寸一分一釐一毫一丝一忽一微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸○七釐九毫四丝七忽九微九纤,为大吕。置大吕半律外周一寸○七釐九毫四丝七忽九微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸○四釐八毫七丝四忽九微二纤,为太蔟。置太蔟半律外周一寸○四釐八毫七丝四忽九微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸○一釐八毫八丝九忽三微三纤,为夹钟。置夹钟半律外周一寸○一釐八毫八丝九忽三微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得九分八釐九毫八丝八忽七微四纤,为姑洗。置姑洗半律外周九分八釐九毫八丝八忽七微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得九分六釐一毫七丝○七微二纤,为仲吕。置仲吕半律外周九分六釐一毫七丝○七微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得九分三釐四毫三丝二忽九微三纤,为蕤宾。置蕤宾半律外周九分三釐四毫三丝二忽九微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得九分○七毫七丝三忽○八纤,为林钟。置林钟半律外周九分○七毫七丝三忽○八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得八分八釐一毫八丝八忽九微四纤,为夷则。置夷则半律外周八分八釐一毫八丝八忽九微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得八分五釐六毫七丝八忽三微七纤,为南吕。置南吕半律外周八分五釐六毫七丝八忽三微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得八分三釐二毫三丝九忽二微八纤,为无射。置无射半律外周八分三釐二毫三丝九忽二微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得八分○八毫六丝九忽六微二纤,为应钟。次求三十六律外径真数。
周求径术,置黄钟倍律外周二寸二分二釐二毫二丝二忽二微二纤,九因,得二尺,以四十除之,得五分,自乘得二十五分,加倍得五十分,为实。开平方法除之,得七分○七毫一丝○六微七纤,是为外径。就置所得为实,依后项乘除之。
径求周术,置黄钟倍律外径七分○七毫一丝○六微七纤,自乘,得五十分。折半,得二十五分,为实。开平方法除之,得五分。以四十乘之,得二尺。九归,得二寸二分二釐二毫二丝二忽二微二纤,是为外周,周径互相求,即还原法也。
置黄钟倍律外径七分○七毫一丝○六微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分八釐六毫九丝七忽六微八纤,为大吕。
置大吕倍律外径六分八釐六毫九丝七忽六微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分六釐七毫四丝一忽九微九纤,为太蔟。置太蔟倍律外径六分六釐七毫四丝一忽九微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分四釐八毫四丝一忽九微七纤,为夹钟。置夹钟倍律外径六分四釐八毫四丝一忽九微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分二釐九毫九丝六忽○五纤,为姑洗。置姑洗倍律外径六分二釐九毫九丝六忽○五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分一釐二毫○二忽六微七纤,为仲吕。置仲吕倍律外径六分一釐二毫○二忽六微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分九釐四毫六丝○三微五纤,为蕤宾。置蕤宾倍律外径五分九釐四毫六丝○三微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分七釐七毫六丝七忽六微三纤,为林钟。置林钟倍律外径五分七釐七毫六丝七忽六微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分六釐一毫二丝三忽一微○,为夷则。
置夷则倍律外径五分六釐一毫二丝三忽一微○为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分四釐五毫二丝五忽三微八纤,为南吕。置南吕倍律外径五分四釐五毫二丝五忽三微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分二釐九毫七丝三忽一微五纤,为无射。置无射倍律外径五分二釐九毫七丝三忽一微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分一釐四毫六丝五忽一微一纤,为应钟。置应钟倍律外径五分一釐四毫六丝五忽一微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分,为黄钟。
置黄钟正律外径五分为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分八釐五毫七丝六忽五微九纤,为大吕。置大吕正律外径四分八釐五毫七丝六忽五微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分七釐一毫九丝三忽七微一纤,为太蔟。置太蔟正律外径四分七釐一毫九丝三忽七微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分五釐八毫五丝○二微○,为夹钟。
置夹钟正律外径四分五釐八毫五丝○二微○为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分四釐五毫四丝四忽九微三纤,为姑洗。置姑洗正律外径四分四釐五毫四丝四忽九微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分三釐二毫七丝六忽八微二纤,为仲吕。置仲吕正律外径四分三釐二毫七丝六忽八微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分二釐○四丝四忽八微二纤,为蕤宾。置蕤宾正律外径四分二釐○四丝四忽八微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分○八毫四丝七忽八微八纤,为林钟。置林钟正律外径四分○八毫四丝七忽八微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分九釐六毫八丝五忽○二纤,为夷则。置夷则正律外径三分九釐六毫八丝五忽○二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分八釐五毫五丝五忽二微七纤,为南吕。置南吕正律外径三分八釐五毫五丝五忽二微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分七釐四毫五丝七忽六微七纤,为无射。置无射正律外径三分七釐四毫五丝七忽六微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分六釐三毫九丝一忽三微二纤,为应钟。置应钟正律外径三分六釐三毫九丝一忽三微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分五釐三毫五丝五忽三微三纤,为黄钟。置黄钟半律外径三分五釐三毫五丝五忽三微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分四釐三毫四丝八忽八微四纤,为大吕。置大吕半律外径三分四釐三毫四丝八忽八微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分三釐三毫七丝○九微九纤,为太蔟。置太蔟半律外径三分三釐三毫七丝○九微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分二釐四毫二丝○九微八纤,为夹钟。置夹钟半律外径三分二釐四毫二丝○九微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分一釐四毫九丝八忽○二纤,为姑洗。置姑洗半律外径三分一釐四毫九丝八忽○二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分○六毫○一忽三微三纤,为仲吕。置仲吕半律外径三分○六毫○一忽三微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分九釐七毫三丝○一微七纤,为蕤宾。置蕤宾半律外径二分九釐七毫三丝○一微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分八釐八毫八丝三忽八微一纤,为林钟。
置林钟半律外径二分八釐八毫八丝三忽八微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分八釐○六丝一忽五微五纤,为夷则。
置夷则半律外径二分八釐○六丝一忽五微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分七釐二毫六丝二忽六微九纤,为南吕。
置南吕半律外径二分七釐二毫六丝二忽六微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分六釐四毫八丝六忽五微七纤,为无射。
置无射半律外径二分六釐四毫八丝六忽五微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分五釐七毫三丝二忽五微五纤,为应钟。次求三十六律内径真数。
先置黄钟倍律通长二尺为实,四十除之,得五分,是为内径。就置所得为实,依后项乘除之。
置黄钟倍律内径五分为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分八釐五毫七丝六忽五微九纤,为大吕。置大吕倍律内径四分八釐五毫七丝六忽五微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分七釐一毫九丝三忽七微一纤,为太蔟。置太蔟倍律内径四分七釐一毫九丝三忽七微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分五釐八毫五丝○二微○,为夹钟。
置夹钟倍律内径四分五釐八毫五丝○二微○为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分四釐五毫四丝四忽九微三纤,为姑洗。置姑洗倍律内径四分四釐五毫四丝四忽九微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分三釐二毫七丝六忽八微二纤,为仲吕。置仲吕倍律内径四分三釐二毫七丝六忽八微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分二釐○四丝四忽八微二纤,为蕤宾。置蕤宾倍律内径四分二釐○四丝四忽八微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得四分○八毫四丝七忽八微八纤,为林钟。置林钟倍律内径四分○八毫四丝七忽八微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分九釐六毫八丝五忽○二纤,为夷则。置夷则倍律内径三分九釐六毫八丝五忽○二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分八釐五毫五丝五忽二微七纤,为南吕。置南吕倍律内径三分八釐五毫五丝五忽二微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分七釐四毫五丝七忽六微七纤,为无射。置无射倍律内径三分七釐四毫五丝七忽六微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分六釐三毫九丝一忽三微二纤,为应钟。置应钟倍律内径三分六釐三毫九丝一忽三微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分五釐三毫五丝五忽三微三纤,为黄钟。置黄钟正律内径三分五釐三毫五丝五忽三微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分四釐三毫四丝八忽八微四纤,为大吕。
置大吕正律内径三分四釐三毫四丝八忽八微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分三釐三毫七丝○九微九纤,为太簇。
置太簇正律内径三分三釐三毫七丝○九微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分二釐四毫二丝○九微八纤,为夹钟。
置夹钟正律内径三分二釐四毫二丝○九微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分一釐四毫九丝八忽○二纤,为姑洗。
置姑洗正律内径三分一釐四毫九丝八忽○二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得三分○六毫○一忽三微三纤,为仲吕。
置仲吕正律内径三分○六毫○一忽三微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分九釐七毫三丝○一微七纤,为蕤宾。置蕤宾正律内径二分九釐七毫三丝○一微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分八釐八毫八丝三忽八微一纤,为林钟。置林钟正律内径二分八釐八毫八丝三忽八微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分八釐○六丝一忽五微五纤,为夷则。置夷则正律内径二分八釐○六丝一忽五微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分七釐二毫六丝二忽六微九纤,为南吕。置南吕正律内径二分七釐二毫六丝二忽六微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分六釐四毫八丝六忽五微七纤,为无射。置无射正律内径二分六釐四毫八丝六忽五微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分五釐七毫三丝二忽五微五纤,为应钟。
置应钟正律内径二分五釐七毫三丝二忽五微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分五釐,为黄钟。
置黄钟半律内径二分五釐为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分四釐二毫八丝八忽二微九纤,为大吕。置大吕半律内径二分四釐二毫八丝八忽二微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分三釐五毫九丝六忽八微五纤,为太蔟。置太蔟半律内径二分三釐五毫九丝六忽八微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分二釐九毫二丝五忽一微○,为夹钟。
置夹钟半律内径二分二釐九毫二丝五忽一微○为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分二釐二毫七丝二忽四微六纤,为姑洗。置姑洗半律内径二分二釐二毫七丝二忽四微六纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分一釐六毫三丝八忽四微一纤,为仲吕。置仲吕半律内径二分一釐六毫三丝八忽四微纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分一釐○二丝二忽四微一纤,为蕤宾。置蕤宾半律内径二分一釐二丝二忽四微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得二分○四毫二丝三忽九微四纤,为林钟。置林钟半律内径二分○四毫二丝三忽九微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一分九釐八毫四丝二忽五微一纤,为夷则。置夷则半律内径一分九釐八毫四丝二忽五微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一分九釐二毫七丝七忽六微三纤,为南吕。置南吕半律内径一分九釐二毫七丝七忽六微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一分八釐七毫二丝八忽八微三纤,为无射。置无射半律内径一分八釐七毫二丝八忽八微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一分八釐一毫九丝五忽六微六纤,为应钟。次求三十六律内周真数。
径求周术,置黄钟倍律内径五分,自乘,得二十五分。折半,得一十二分半,为实。开平方法除之,得三分五釐三毫五丝五忽三微三纤九尘。以四十乘之,得一尺四寸一分四釐二毫一丝三忽五微六纤。九归,得一寸五分七釐一毫三丝四忽八微四纤,是为内周。就置所得为实,依后项乘除之。周求径术,置黄钟倍律内周一寸五分七釐一毫三丝四忽八微四纤,九因,得一尺四寸一分四釐二毫一丝三忽五微六纤。以四十除之,得三分五釐三毫五丝五忽三微三纤九尘,自乘,得一十二分半。加倍,得二十五分,为实。开平方法除之,得五分,是为内径。周径互相求,即还原法也。
置黄钟倍律内周一寸五分七釐一毫三丝四忽八微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸五分二釐六毫六丝一忽五微一纤,为大吕。置大吕倍律内周一寸五分二釐六毫六丝一忽五微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸四分八釐三毫一丝五忽五微三纤,为太蔟。置太蔟倍律内周一寸四分八釐三毫一丝五忽五微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸四分四釐○九丝三忽二微八纤,为夹钟。
置夹钟倍律内周一寸四分四釐○九丝三忽二微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸三分九釐九毫九丝一忽二微二纤,为姑洗。置姑洗倍律内周一寸三分九釐九毫九丝一忽二微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸三分六釐○○五忽九微四纤,为仲吕。置仲吕倍律内周一寸三分六釐○○五忽九微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸三分二釐一毫三丝四忽一微二纤,为蕤宾。置蕤宾倍律内周一寸三分二釐一毫三丝四忽一微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸二分八釐三毫七丝二忽五微二纤,为林钟。置林钟倍律内周一寸二分八釐三毫七丝二忽五微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸二分四釐七毫一丝八忽○○,为夷则。
置夷则倍律内周一寸二分四釐七毫一丝八忽○○为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸二分一釐一毫六丝七忽五微二纤,为南吕。置南吕倍律内周一寸二分一釐一毫六丝七忽五微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸一分七釐七毫一丝八忽一微二纤,为无射。置无射倍律内周一寸一分七釐七毫一丝八忽一微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸一分四釐三毫六丝六忽九微一纤,为应钟。置应钟倍律内周一寸一分四釐三毫六丝六忽九微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸一分一釐一毫一丝一忽一微一纤,为黄钟。置黄钟正律内周一寸一分一釐一毫一丝一忽一微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸○七釐九毫四丝七忽九微九纤,为大吕。置大吕正律内周一寸○七釐九毫四丝七忽九微九纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸○四釐八毫七丝四忽九微二纤,为太蔟。置太蔟正律内周一寸○四釐八毫七丝四忽九微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得一寸○一釐八毫八丝九忽三微三纤,为夹钟。置夹钟正律内周一寸○一釐八毫八丝九忽三微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得九分八釐九毫八丝八忽七微四纤,为姑洗。置姑洗正律内周九分八釐九毫八丝八忽七微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得九分六釐一毫七丝○七微二纤,为仲吕。置仲吕正律内周九分六釐一毫七丝○七微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得九分三釐四毫三丝二忽九微三纤,为蕤宾。置蕤宾正律内周九分三釐四毫三丝二忽九微三纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得九分○七毫七丝三忽○八纤,为林钟。置林钟正律内周九分○七毫七丝三忽○八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得八分八釐一毫八丝八忽九微四纤,为夷则。置夷则正律内周八分八釐一毫八丝八忽九微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得八分五釐六毫七丝八忽三微七纤,为南吕。置南吕正律内周八分五釐六毫七丝八忽三微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得八分三釐二毫三丝九忽二微八纤,为无射。置无射正律内周八分三釐二毫三丝九忽二微八纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得八分○八毫六丝九忽六微二纤,为应钟。置应钟正律内周八分○八毫六丝九忽六微二纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得七分八釐五毫六丝七忽四微二纤,为黄钟。置黄钟半律内周七分八釐五毫六丝七忽四微二纤为实,以十亿乘之,以十亿 二千九百三十万○二千二百三十六除之,得七分六釐一毫三丝○七微五纤,为大吕。置大吕半律内周七分六釐三毫三丝○七微五纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得七分四釐一毫五丝七忽七微六纤,为太蔟。置太蔟半律内周七分四釐一毫五丝七忽七微六纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得七分二釐○四丝六忽六微四纤,为夹钟。置夹钟半律内周七分二釐○四丝六忽六微四纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分九釐九毫九丝五忽六微一纤,为姑洗。置姑洗半律内周六分九釐九毫九丝五忽六微一纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分八釐○○二忽九微七纤,为仲吕。置仲吕半律内周六分八釐○○二忽九微七纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分六釐○六丝七忽○六纤,为蕤宾。
置蕤宾半律内周六分六釐○六丝七忽○六纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分四釐一毫八丝六忽二微六纤,为林钟。置林钟半律内周六分四釐一毫八丝六忽二微六纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分二釐三毫五丝九忽○○,为夷则。
置夷则半律内周六分二釐三毫五丝九忽○○为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得六分○五毫八丝三忽七微六纤,为南吕。置南吕半律内周六分○五毫八丝三忽七微六纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分八釐八毫五丝九忽○六纤,为无射。置无射半律内周五分八釐八毫五丝九忽○六纤为实,以十亿乘之,以十亿○二千九百三十万○二千二百三十六除之,得五分七釐一毫八丝三忽四微五纤,为应钟。