钦定古今图书集成经济汇编乐律典
第五十九卷目录
律吕部汇考十三
明唐荆川稗编〈求元声法 制管之法 十二宫去其中管为七 头管即古管〉
韩苑洛志乐一〈律吕说 律吕直解 黄钟分寸图 黄钟管图 林钟管图 大蔟管图 南吕管图 姑洗管图 应钟管图 蕤宾管图 大吕管图 夷则管图 夹钟管图 无射管图 仲吕管图〉
明唐荆川稗编〈求元声法 制管之法 十二宫去其中管为七 头管即古管〉
韩苑洛志乐一〈律吕说 律吕直解 黄钟分寸图 黄钟管图 林钟管图 大蔟管图 南吕管图 姑洗管图 应钟管图 蕤宾管图 大吕管图 夷则管图 夹钟管图 无射管图 仲吕管图〉
乐律典第五十九卷
律吕部汇考十三
《明唐荆州稗编》求元声法《律书》曰:黄钟之实,十七万七千一百四十七,管长九寸,是十二律之管,惟黄钟之宫为最长,故谓之元声。犹言头一声也。然所谓九寸者,非度之以凡尺,本乎人声而得之也。其法,令歌者作声,取其最下一声,而以竹长九寸,上下空围九方分者为管,吹其体中翕声以效之,视管声比人声稍高,则增管令长,比人声稍下,则减管令短。上下游移以裁之,必其与人声合一而无差,乃以此管命为九寸黄钟之宫也。次以子谷秬黍中者一千二百粒,实管中,视黍不足则易管令小,有馀则易管令大,以此管命为黄钟径围,是谓以声生律,以律生尺,而元声在是矣。此管体中翕声,谓之合字,以合字写之琴瑟第一弦,钟磬第一板,篪笛第一孔,笙竽第一簧,则八音皆正。以此管上下相生,即得已后十一律,而律吕皆正。宋儒程颢曰:清者极吹尽清,浊者极吹尽浊。向中间折取一声,即口中声,盖以黄钟之半律为中声也。其法与此同。
制管之法
元不师古,无足道者,惟太史院景表尺,乃郭守敬所造。守敬精于律历,决非苟作。今钦天监表尺是也。比市尺,只得八寸强。愚尝取黑黍,拣其中者一千二百粒,日乾之,称重五钱者,以九十粒横累之,命为九寸,与表尺合。又截竹为管,长同黍寸,其窍上下均容一千二百黍者,吹之,其声与人之最下一声合,是为黄钟之声。制管之法,可谓简易而无难矣。黄钟宫俗呼正宫 商俗呼大石调
角俗呼大石角调 羽俗呼般涉调
大吕宫俗呼高宫 商俗呼高大石调
角俗呼高大石角 羽俗呼高般涉
太簇宫俗呼中管高宫 商俗呼中管高大石角俗呼中管高大石角 羽俗呼中管高般涉夹钟宫俗呼中吕宫 啇俗呼双调角俗呼双调角 羽俗呼中吕调
姑洗宫俗呼中管中吕宫 啇俗呼双调角俗呼中管双角调 羽俗呼中吕调
仲吕宫俗呼道调宫 商俗呼小石调
角俗呼小石角调 羽俗呼正平调
蕤宾宫俗呼中管道调宫 商俗呼中管小石调角俗呼中管小石角调 羽俗呼中管正平调林钟宫俗呼南吕宫 商俗呼歇指调
角俗呼歇指角调 羽俗呼高平调
夷则宫俗呼仙吕宫 商俗呼商调
角俗呼商角调 羽俗呼仙吕调
南吕宫俗呼中管仙吕宫 商俗呼中管商调角俗呼中管商角调 羽俗呼中管仙吕调无射宫俗呼黄钟宫 商俗呼越调
角俗呼越角调 羽俗呼羽调
应钟宫俗呼中管黄钟宫 商俗呼中管越调角俗呼中管越角调 羽俗呼中管羽调。
十二宫去其中管为七
臣按十二宫用七,去其中管而言也。自子黄钟,至亥应钟,十二宫各具七声,共八十四声。内寅太簇七声,与丑大吕七声同字谱,宫声同四字,商声同一字,角声同上勾,徵声同工字,羽声同凡字。辰姑洗七声与卯夹钟七声同字谱,宫声同一字,商声同上勾,徵声同凡字。惟角羽二声有尺工六五之异,酉南吕七声与申夷则七声同字谱,宫声同工字,商声同凡字,徵声同一字,羽声同上勾,惟角声有六五之异。午蕤宾亥应钟亦各七声,虽与前位不同,然黄钟均内以蕤宾为变徵,应钟为变宫,二变名曰和谬,不可为调。已上五宫,共五七三十五调,皆以中管名之。中管云者,谓其声在前后二律之间,而与前律同出一孔,以之制调音韵重,虽强易其名,终无所表异,视前律为不逮,故不用也。十二宫,除此外,七宫而已。唐祖孝孙参定雅乐古钟十二,近代惟用其七,馀五钟,仍号哑钟,莫能通者。张文收吹律调之,五钟皆响彻。盖钟无不响者,以不用,故以哑名之。随管击之,宁得不应。当时盖未考中管之说耳。头管即古管
头管九孔,自下而上,管体中翕然为合字第一孔,四字第二孔,一字第三孔,生字第四孔。后出勾字第五孔,尺字第六孔,工字第七孔,凡字第八孔。后出六字第九孔。五字大乐,以此先诸乐,谓之头管,经曰:嘒嘒管,声下管,象武之类是也。管色字谱五,凡、工、尺、上、四,六一勾合管九孔,六勾二字,并后出合字,在管体中,自下而上,合字为黄钟正声,下四大吕,高四太簇,共第一孔。下一夹钟,高一姑洗,共第二孔。上字仲吕,第三孔。勾字蕤宾,后出第四孔。尺字林钟,第五孔。下工夷则,高工南吕,共第六孔。下凡无射,高凡应钟,共第七孔。六字黄钟清后出第八孔。下五大吕清,高五太簇清,紧五夹钟清,共第九孔。九孔内,四一工凡皆有高下二声,五字有高下紧三声,惟上勾尺无高下,盖仲蕤林三律,不分清浊,自然应律也。十字者,载籍无可考,惟《楚辞·大招》曰:二八接武,投诗赋只,叩钟调磬,娱人乱只,四上竞气,极声变只。注曰:四上,未详。今按《招魂》曰:吴歈蔡讴奏大吕,些大吕为宫,其谱下四,仲吕为角。其谱上字,四上竞气。谓宫角相应也。
《韩苑洛志乐一》律吕说
《陈氏乐书》曰:甚哉,诸儒之论律吕,何其纷纷邪。谓阴阳相生,自黄钟始,而左旋八,八为伍,管以九寸为法者,班固之说也。生倍实上生四实,皆三其法,而管又不专以九寸为法者,司马迁之说也。持隔九相生之说,以中吕上生黄钟,不满九寸,谓之执始,下生去灭,上下相生,终于南事十二律之外,更增六八为六十律者,京房之说也。本吕览淮南王安、蔡邕之说,建蕤宾重上生之议,至于大吕、夹钟、仲吕之律所生分等,又皆倍焉者,郑康成之说也。隔七为上生,隔八为下生,至于仲吕,则孤而不偶,蕤宾则踰次无准者,刘向之说也。演京房南事之馀,而伸之为三百六十律,日当一管,各以次生者,宋钱乐之之说也。斥京房之说,而以新旧法分度参录之者,何承天、沈约之说也。校定黄钟,每律减三分,而以七寸为法者,隋刘焯之论也。析毫釐之彊弱为算者,梁武帝之法也。由此观之,诸儒之论角立蜂起,要之最为精密者,班固之志而已。今夫阴阳之声,上生者三分之外益一,下生者三分之内损一,盖古人简易之法,犹古历周天三百六十五度四分度之一也。若夫律同之声,适多寡之数,长短之度,小大之量,清浊之音,一要宿乎中声而止,则动黄钟而林钟应,动无射而仲吕应,和乐未有不兴者矣。黄钟距地面有浅深,必也洛阳乎天地之中,阴阳之会也,然后浅深之应的。律不求元声元气,虽能宰物,终是苟且,与天地何与。然圣人得元声以候元气,今当候元气以求元声。律能应气,度量衡由之而定。凡八音之轻重、厚薄、大小、多寡、长短,由于律其体,则天地之体,宜其用之能感天地也。
圣人不能以一身周天下之用,故制为器数,以教万世。是以天下后世人,非圣人而道,则圣人之道也。昔孔子闻韶于齐,夫其考击而搏拊者,固非皆夔伦也。而其美如此者,器数存也。且圣人之道,有文,有本。天地之道,有纤,有洪。自然之理也。今不论度量衡之数,而曰妙在其人,则圣人当时,止为一支之木,一块之土,一钩之金,足矣。何必为钟、为鼓、为笙、为磬,又从而为篁、为弦、有烦、有简若是哉。今试以祭祀之时,燕享之际,琴瑟缺其弦,笙尽去其篁,铸万钧为镈钟,合以方寸之鼗鼓,又从而尽去八音,使宝常击食器,荀勖摇牛铎,可乎,不可乎。是故君子不为无益之空言,必究制作之实用。
自隋唐以来,律皆造作,用金刀剖削而成,非本然之管,恐伤元气。且律吕丝忽所争,若非良工剖削之际,安能适中。予谓多取竹管,其从长未免用刀断之,必求径三分四釐六毫,周广十分三釐六毫者,而后用之,庶得声气之元矣。律虽非生于累黍,然古乐既亡,律管非累黍,亦何由定。予谓亦须自九十黍,累为九寸,然后依蔡氏之说,多截竹管,或长一分,或半分,或十分分之一,以至于九。或短一分,或半分,或十分分之一,以至于九。中间必有适之者矣。
埋管之地,不可以城市之中。盖城市之地,翻取数过,皆灰粪瓦砾,非本然之土。必于旷野素无人居之地土之黄壤者,亦须去二三尺,以尽客土,撅亦不可深,深则恐伤正气。如此候之,或得正气之应矣。
器与造化通,唯律而已。黄钟既定,凡天地之器,虽衣服盘盂,皆造化之运,形而上,形而下,本一物也。明律义,凡天下之理,皆可通,不但为作乐而已。太极之理,亦不外此也。
八音之数,惟丝为自然。其七音皆倚此而起数,丝忽之际,其微矣乎。
春阳无不到,陵原无二气。蕤宾隔八,若益一分上生大吕,与损一分下生大吕,倍其数,长短不差丝毫。然不如下生为自然,于十二律之序为顺,审思自见。
大吕当为十月管,逆数至应钟为夏至。
今尺惟车工之尺最准,万家不差毫釐,少不似则不利载,是孰使之然哉。古今相沿,自然之度也。然今之尺,则古之尺二寸也。所谓尺二之轨,天下皆同是也。以木工尺去二寸,则周尺也。昔鲁公欲高大其宫室,而畏王制,乃以时尺增一寸,召班授之。班知其意,后增一寸,进于公曰:臣家相传之尺,乃舜时同度之尺也。乃以其尺为之度。诸侯闻之,争召班。然班亦本木工之圣者也。
世儒有言,学乐必先等字,若然三百篇,无一章中律者,经言律和声,未闻以律就声也。夫人之声,有洪者,细者,亮者,万万不齐。古之圣人,虽尧舜之声,亦不能合律。惟大禹一人声可为律耳。正使人人之声皆中律,亦只五声。人有八十四喉舌,且如呦呦鹿鸣一句,上呦字宫,下呦字徵,岂一字二音哉。协以就律耳等字云者,非知乐者之言也。先儒之论律吕,正声倍子而为母,子声半正而为子。若黄钟之管正声,九寸为均,其子声则四寸半。三分损一,下生林钟之子,又三分益一,上生太簇之子。由是第之,终于中吕,以从十二母相生之法。故黄钟为宫,而下生林钟为徵,林钟上生太簇为商,太簇下生南吕为羽,南吕上生姑洗为角,此黄钟之调,皆得三分之次,故用正律之声。大吕为宫,而下生夷则为徵,夷则上生夹钟为商,夹钟下生无射为羽,无射上生中吕为角,此大吕之调,皆得三分之次,故用正律之声。太簇为宫,而下生南吕为徵,南吕上生姑洗为商,姑洗下生应钟为羽,应钟上生蕤宾为角,此太簇之调,皆得三分之次,故用正律之声。夹钟为宫,而下生无射为徵,无射上生中吕为商,中吕上生黄钟为羽,黄钟正律声长,非中吕,三分去一之次,故用子声为羽。黄钟下生林钟为角,林钟子律声短,非中吕为商之次,故还用正声为角,此夹钟之调,正声四,子声一也。姑洗为宫,而下生应钟为徵,应钟上生蕤宾为商,蕤宾上生大吕为羽,大吕正律声,非蕤宾三分去一之次,故用子声为羽。大吕下生夷则为角,夷则子律声短,非蕤宾为商之次,故还用正声为角。此姑洗之调,正声四,子声一也。中吕为宫,而上生黄钟为徵,黄钟正律声长,非中吕三分去一之次,故用子声为徵。黄钟下生林钟为商,林钟子律声短,非中吕为宫之次,故还用正声为商。林钟上生太簇为羽,太簇正律声长,非林钟三分去一之次,故用子声为羽。太簇下生南吕为角,此中吕之调,正声三,子声二也。蕤宾为宫,而上生大吕为徵,大吕正律声长,非蕤宾三分去一之次,故用子声为徵。大吕下生夷则为商,夷则上生夹钟为羽,夹钟正律声长,非夷则三分去一之次,故用子声为羽。夹钟下生无射为角,无射子律声短,非夷则为商之次,故还用正声为角。此蕤宾之调,正声三,子声二也。林钟为宫,而上生太簇为徵,太簇正律声长,非林钟三分去一之次,故用子声为徵。太簇下生南吕为商,南吕上生姑洗为羽,姑洗正律声长,非南吕三分去一之次,故用子声为羽。姑洗下生应钟为角,应钟子律声短,非南吕为商之次,故还用正声为角。此林钟之调,正声三,子声二也。夷则为宫,而上生夹钟为徵,夹钟正律声长,非夷则三分去一之次,故用子声为徵。夹钟下生无射为商,无射子律声短,非夷则为宫之次,故还用正声为商。无射上生中吕为羽,中吕正律声长,非无射三分去一之次,故用子声为羽。中吕上生黄钟为角,黄钟正律声长,非无射为商之次,故用子声为角。此夷则之调,正声二,子声三也。南吕为宫,南吕上生姑洗为徵,姑洗正律声长,非南吕三分去一之次,故用子声为徵。姑洗下生应钟为商,应钟子律声短,非南吕为宫之次,故用正声为商。应钟上生蕤宾为羽,蕤宾正律声长,非应钟三分去一之次,故用子声为羽。蕤宾上生大吕为角,大吕正律声长,非应钟为商之次,故用子声为角。此南吕之调,正声二,子声三也。无射为宫,而上生中吕为徵,中吕正律声长,非无射三分去一之次,故用子声为徵。中吕上生黄钟为商,黄钟正律声长,非无射为宫之次,故用子声为商。黄钟下生林钟为羽,林钟正律声长,非黄钟子声三分去一之次,故用子声为羽。林钟上生太簇为角,太簇正律声长,非黄钟子声为商之次,故用子声为角。此无射之调,正声一,子声四也。应钟为宫,应钟上生蕤宾为徵,蕤宾正律声长,非应钟三分去一之次,故用子声为徵。蕤宾上生大吕为商,大吕正律声长,非应钟为宫之次,故用子声为商。大吕下生夷则为羽,夷则正律声长,非蕤宾子声为徵之次,故用子声为羽。夷则上生夹钟为角,夹钟正律声长,非大吕子声为商之次,故用子声为角。此应钟之调,正声一,子声四也。凡此蔽于十二律均旋为宫之说,失《周礼》三宫之意也。三宫旋相而唱和有应,曷尝有子声邪。若以为十二律皆有子声,然则黄钟、大吕、太簇三律,何独止用正声邪。
律吕直解
黄钟第一。解曰:此黄钟之体数也。十分为寸,分釐毫丝并同,断用之,九以为十,何。以十,自然之数也。长九寸,空围九分,积八百一十分。
解曰:从长九寸,寸者十分,黄钟之长,通有九寸也。空围九分,分者十分寸之一,黄钟之管满于围中,容九方分也。积实八十一分,黄钟之管,从长九寸,寸十分,黄钟九十分,空围中九分,每长一分,围必九分,以九十因之,则八百一十分也。
黄钟分寸图黄钟分寸图

员田术,三分益一,得十二分。
解曰:三分为一分,三分,九分也。又益一分,共四分,十二分也。以九方分平置,又三分益一分,共十二方分。
以开方法除之。
解曰:以上一分,分割为四片,每片二釐五毫,贴于九方分四面。又每片除一毫九丝二忽为角,每片上得二釐三毫八忽。
得三分四釐六毫强,为实径之数。
解曰:中九方分,四面各得三分,外四面各二釐三毫八忽,东与西四釐六毫一丝六忽,南与北亦然。是其纵横,又得三分四釐六毫一丝六忽,为实径之数。
不尽三毫八丝四忽。
解曰:此补四角之数也。本以一分割作四片,每片二釐五毫,两面该五釐,合九方分,该三分五釐径。今每片取一毫九丝二忽,补角两面,该三毫八丝四忽径,止得三分四釐六毫一丝六忽,犹馀三毫八丝四忽也。
今求圆积之数。
解曰:谓围圆之数,并内积之数也。
以径三分四釐六毫自相乘。
解曰:不用一丝六忽,每一分得三分四釐六毫,每一釐得三釐四毫六丝,每一毫得三毫四丝六忽。〈分以三乘釐以四乘毫以六乘〉
得十一分九釐七毫一丝六忽。
解曰:若用一丝六忽,时正十二方分,惟不用一丝六忽,故止得如此。以上所乘计之分之,所得者十分三釐八毫釐之,所得者一分三釐八毫四丝毫之,所得者二釐六丝十六忽,总计所得十一方分零九釐七毫一丝六忽。
加以开方不尽之数二毫八丝四忽,
解曰:此不尽之数,与上不同。上不尽之数,乃是以三分四釐六毫一丝六忽,为径不尽三毫八丝四忽,除去补四角,成十二方分。此不尽之数,乃是以三分四釐六毫为径,于十二方分中馀得此数。
得一十二分,
解曰:以十一分九釐七毫一丝六忽,合二毫八丝四忽,共得十二方分,如前开方之数。
以管长九十分乘之,得一千八十分为方积之数。
解曰:每管一分,该十二分,积九十分而计之,共一千八十分,为方积之数。径三分四釐六毫一丝六忽,周方共十三分八釐四毫六丝四忽。
四分取三,为圆积之数,得八百一十分。
解曰:以一千八十分作四分,则一分该二百七十分四分中,取三分为圆积之数。该八百一十分以九方分积中计之,径三分四釐六毫一丝六忽,周圆十分八釐三毫四丝八小忽○八秒。〈蔡十分三釐八毫则少彭十分八釐七毫则多〉
彭氏曰:黄钟律管,有从长,有面羃,有空围,有周,有径,有积实。
解曰:从长者,只以黄钟管上下言之,不以积论也。一一管,二九寸,三九十分,四九百釐,五九千毫,六九万丝。面羃者,上论黄钟管面上中郛之数也。空
围者,论围圆中所容之数,合面羃积实之数也。以方分计之,一分整,四分有馀,四分不足,以有馀补不足,每长一分当有九方分,充满于黄钟之管。周广者,九方分之郛,黄钟管周圆之数也。当有十分八釐三毫四丝零八小忽○八秒。径者,论黄钟管直径之数也。以管三分得一,当有三分四釐六毫一丝六忽。内积者,论黄钟管上下空围中之数也。七九为丝法,八九十为毫法,九九百为釐法,十九千为分法,十一九万为寸法,十二八十一万为黄钟之实,通计黄钟之实,一管九寸九十分,乘空围九分八百一十分,八十一万釐,八万万一千万毫,八千万万一百万万丝。
积黍,
解曰:一为一分,黄钟之管长九十分,立九十黍,每一分空围中可容十三黍,又三分黍之一,以九十因之,可容千二百黍矣。夫黄钟之管,一黍为一分,黄钟之实,止八百一十方分,何以能容千二百黍哉。盖方与圆不同,方无空,圆有空,以圆顶对圆顶,则一为一分。若纵横补塞其空,充满于黄钟之管,可容千二百黍。九十分之,则每分该十三黍又三分黍之一矣。用羊头山黍,以筛子筛之,去其大者、小者,而用中者。若管既定,则随大小之宜而实其数,尤为至当。
黄钟之实第二。解曰:此黄钟之用数也。九分为寸,分釐毫丝并同。约体之十以为九,何。以九因三分损益而立也。若以十,则三分不尽其数,必有馀剩之数,且难推算。约之为九,既不失其十之长,又无馀剩之数,易于推算矣。又置一而三,三住而九间之,亦理之自然也。
子一 黄钟之律。
解曰:此黄钟通长之管也。一而已。太极以一含三,此一管含下文寸分釐毫丝之法,数实十一个三也。置一也,阳辰之始也。
丑三 为丝法。
解曰:黄钟之数起于丝,然空围中九分,八面相乘,各三分,每一丝必有三丝,故三为一丝,由一而三,加为三,三个一也。此虽由一而三,然阴阳各为一,事不相涉焉。第一三也,阴辰之始也。
寅九 为寸数。
解曰:此黄钟之九寸也。一管九寸与上寸为一,连事由三,而三加为九,三个三也。第二三也,一寸含三寸。
卯二十七 为毫法。
解曰:黄钟之数,九丝为毫,然一毫乘围,必有三毫,故九三二十七为一毫也。与上丑为一连事,由九而三加为二十七,三个九也。第三三也。
辰八十一 为分数。
解曰:此黄钟八十一分也。一寸九分,九寸共八十一分,与上寅为一连事,由二十七而三,加为八十一,三个二十七也。第四三也。一分含三分。
巳二百四十三 为釐法。
解曰:黄钟之数,九毫为釐。然一釐乘围,必有三釐。二十七既为一毫,则九个二十七,该一百四十三为一釐也。与上卯为一连事,由八十一而三,加为二百四十三,三个八十一也。第五三也。
午七百二十九 为釐数。
解曰:此黄钟七百二十九釐,一分九釐,八十一分共该七百二十九釐,与上辰为一连事,由二百四十三而三,加为七百二十九,三个二百四十三也。第六三也。一釐含三釐。
未二千一百八十七 为分法。
解曰:黄钟之数,九釐为分。然一分乘围必有三分,二百四十三既为一釐,则九个二百四十三,该二千一百八十七为一分也。与上已为一连事,由七百二十九而三,加为二千一百八十七。三个七百二十九也。第七三也。
申六千五百六十一 为毫数。
解曰:此黄钟之六千五百六十一毫也。一釐九毫,七百二十九釐,共该六千五百六十一毫。与上午为一连事,由二千一百八十七而三,加为六千五百六十一,三个二千一百八十七也。第八三也。一毫含三毫也。
酉一万九千六百八十三 为寸法。
解曰:黄钟之数,九分为寸。然一寸乘围必有三寸,二千一百八十七既为一分,则九个二千一百八十七,该一万九千六百八十三为一寸也。与上未为一连事,由六千五百六十一而三,加为一万九千六百八十三,三个六千五百六十一也。第九三也。所谓九三之为寸法是也。
戌五万九千四十九 为丝数。
解曰:此黄钟之五万九千四十九丝也。一毫九丝,
六千五百六十一毫,共该五万九千四十九也。与上申为一连事,由一万九千六百八十三而三,加为五万九千四十九,三个一万九千六百八十三也。第十三也。一丝含三丝。
亥十七万七千一百四十七 为黄钟之实。
解曰:黄钟之数,九寸为管。然乘围而三之,一万九千六百八十三既为一寸,则九个一万九千六百八十三,该十七万七千一百四十七,为九寸一管,黄钟之实也。与上酉为一连事,由五万九千四十九而三,加为十七万七千一百四十七,三个五万九千四十九也。第十一三也。所谓置一而十一,三之为黄钟之实是也。
子、寅、辰、午、申、戌,六阳辰。
解曰:以六律在位故也。子、丑、寅、卯、辰、巳则正阳。
亥、酉、未、巳、卯、丑,六阴辰。
解曰:以六吕在位故也。午、未、申、酉、戌、亥则正阴。黄钟生十一律第三。解曰:十二律相生,亦在内。
黄钟管图缺
子一分 一为九寸。
解曰:子,黄钟也。一,黄钟之管也。下十一律,皆由此管而生。 本注者,黄钟生十一律也。圈外注者,十二律,三分损益相生也。
林钟管图林钟管图

丑三分二 一为三寸。
解曰:丑,林钟也。三分,三分乎子也。二,林钟之管也。以黄钟九寸分为三分,每分三寸,得其二分,计六寸,为林钟之数也。
分黄钟九寸为三分,去一分,下生林钟,得二分,计六寸。
太蔟管图太蔟管图
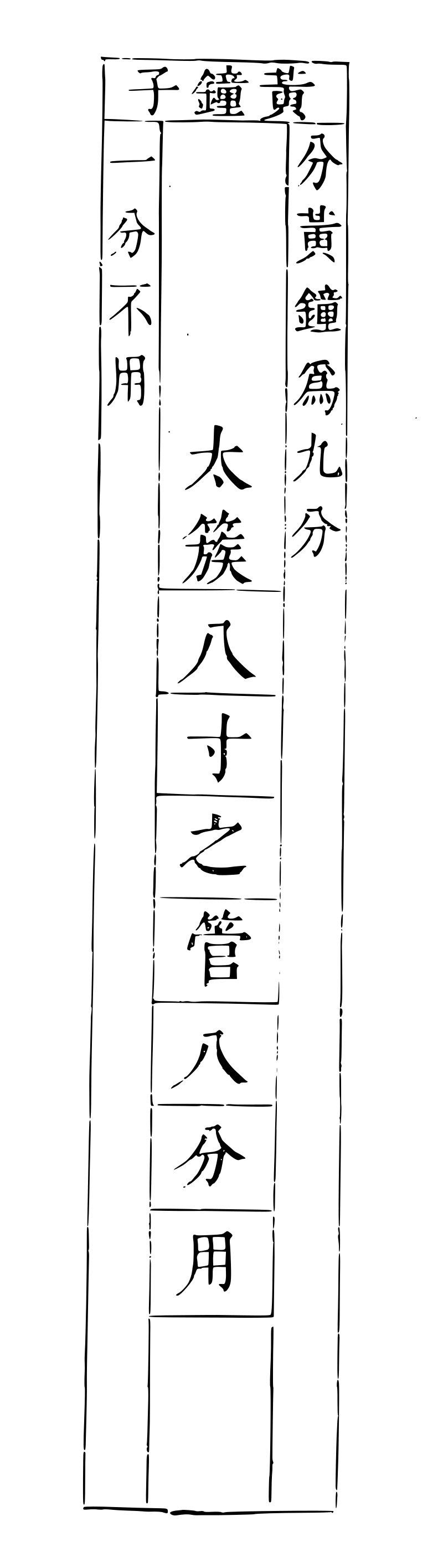
寅九分八 一为一寸。
解曰:寅,太蔟也。九分,九分乎子也。八,太蔟之管也。以黄钟九寸,分为九分,每分一寸,得其八分,计八寸,为太蔟之数也。
分林钟六寸为三分,每分二寸,益一分,上生太蔟,得四分,计八寸。
南吕管图

卯二十七分十六 三为一寸 一为三分。解曰:卯,南吕也。二十七分,二十七分乎子也。十六,南吕之管也。以黄钟九寸,分为二十七分,每三分一寸,得其十六分,计五寸三分,为南吕之数也。分太蔟八寸为三分,每分二寸,六分去一分,下生南吕,得二分,计五寸三分。
姑洗管图姑洗管图

辰八十一分六十四 九为一寸 一为一分。
解曰:辰,姑洗也。八十一分,八十一分乎子也。六十四,姑洗之管也。以黄钟九寸分为八十一分,每九分一寸,得六十四分,计七寸一分,为姑洗之数也。分南吕五寸三分为三分,每分一寸七分,益一分,上生太蔟,得四分,计七寸一分。
应钟管图应钟管图
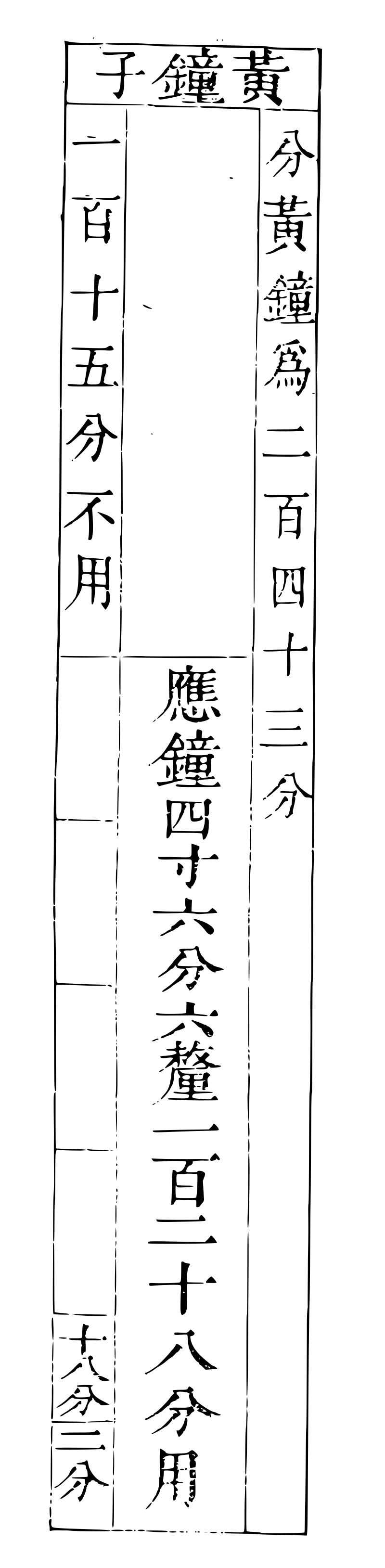
巳二百四十三分一百二十八 二十七为一寸三为一分 一为三釐。
解曰:巳,应钟也。二百四十三分,二百四十三分乎子也。一百二十八,应钟之管也。以黄钟九寸分为二百四十三分,每二十七分一寸,得一百二十八分,计四寸六分六釐,为应钟之数也。
分姑洗七寸一分为三分,每分二寸三分三釐,去一分,下生应钟,得二分,计四寸六分六釐。
蕤宾管图蕤宾管图
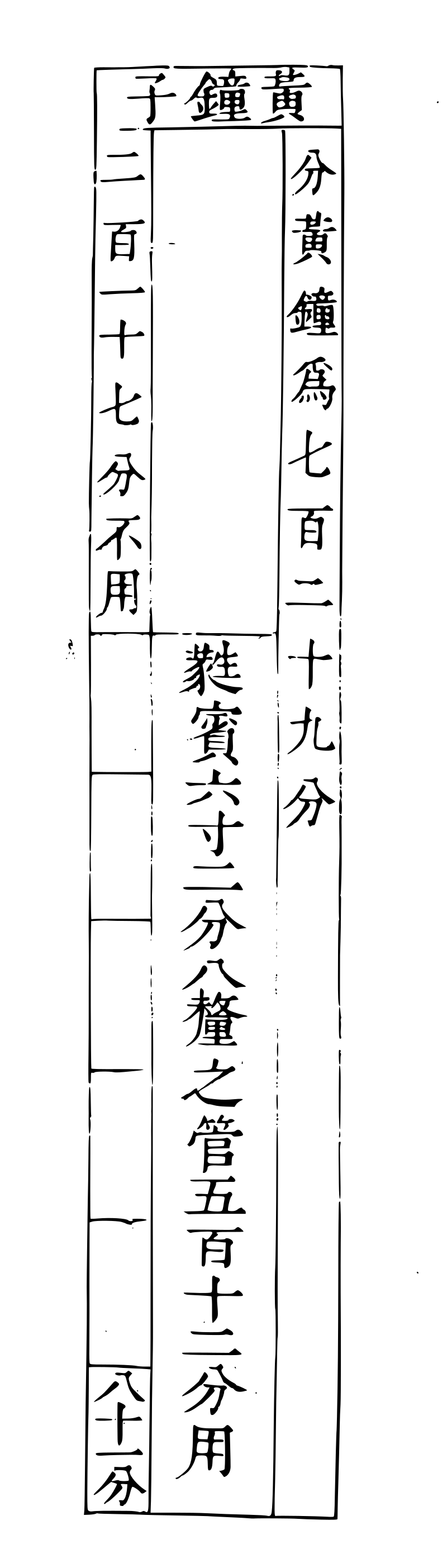
午七百二十九分五百一十二 八十一分为一寸
九为一分 一为一釐。
解曰:午,蕤宾也。七百二十九分,七百二十九分乎子也。五百一十二,蕤宾之管也。以黄钟九寸分为七百二十九分,每八十一分一寸,得五百一十二,计六寸二分八釐,为蕤宾之数也。
分应钟四寸六分六釐为三分,每分一寸五分二釐,益一分,上生蕤宾,得四分,计六寸二分八釐。
大吕管图大吕管图

未二千一百八十七分一千二十四 二百四十三为一寸 二十七为一分 三为一釐 一为三毫。
解曰:未,大吕也。二千一百八十七分,二千一百八十七分乎子也。一千二十四,大吕之半管也。以黄钟九寸分为二千一百八十七分,每二百四十三分一寸,得一千二十四,计四寸一分八釐三毫,在阳,倍之,为八寸三分七釐六毫,为大吕之数也。分蕤宾六寸二分八釐为三分,每分二寸八釐六毫,去一分,下生大吕,得二分,计四寸一分八釐三
毫。在阳,倍之,通计八寸三分七釐六毫。〈在阳谓居五也〉夷则管图毫。在阳,倍之,通计八寸三分七釐六毫。〈在阳谓居五也〉夷则管图

申六千五百六十一分四千九十六 七百二十九为一寸 八十一为一分 九为一釐 一为一毫。
解曰:申,夷则也。六千五百六十一分,六千五百六十一分乎子也。四千九十六,夷则之管也。以黄钟九寸分为六千五百六十一分,每七百二十九分一寸,得四千九十六,计五寸五分五釐一毫,为夷则之数也。
分大吕四寸一分八釐三毫为三分,每分一寸三分五釐七毫,益一分,上生夷则,得四分,计五寸五分五釐一毫。
夹钟管图夹钟管图

酉一万九千六百八十三分八千一百九十二 二千一百八十七为寸 二百四十三为一分 二十七为一釐 三为一毫 一为二丝。
解曰:酉,夹钟也。一万九千六百八十三分,一万九千六百八十三分乎子也。八千一百九十二,夹钟之半管也。以黄钟九寸,分为一万九千六百八十三分,每二千一百八十七为一寸,得八千一百九十二,计三寸六分六釐三毫六丝。在阳,倍之,共七寸四分三釐七毫三丝,为夹钟之数也。
分夷则五寸五分五釐一毫为三分,每分一寸七分七釐六毫三丝,去一分,下生夹钟,得二分,计三寸六分六釐三毫六丝。在阳,倍之,通计七寸四分三釐七毫三丝也。〈在阳谓居卯也〉
无射管图无射管图

戌五万九千四十九分三万二千七百六十八 六千五百六十一为一寸 七百二十九为一分 八十一为一釐 九为一毫 一为一丝。
解曰:戌,无射也。五万九千四十九分,五万九千四十九分乎子也。三万二千七百六十八,无射之管也。以黄钟九寸,分为五万九千四十九分,每六千五百六十一为一寸,得三万二千七百六十八,计四寸八分八釐四毫八丝,为无射之数也。
分夹钟三寸六分六釐三毫六丝为三分,每分一
寸二分二釐一毫二丝,益一分,上生无射,得四分,计四寸八分八釐四毫八丝。
仲吕管图仲吕管图

亥一十七万七千一百四十七分六万五千五百三十六一万九千六百八十三为一寸 二千一百八十七为一分 二百四十三为一釐 二十七为一毫 三为一丝 一为一忽。
解曰:亥,仲吕也。十七万七千一百四十七分,十七万七千一百四十七分乎子也。六万五千五百三十六,仲吕之半管也。以黄钟九寸,分为十七万七千一百四十七分,每一万九千六百八十三为一寸,得六万五千五百三十六,计三寸二分八釐六毫二丝三忽,在阳,倍之,共六寸五分八釐三毫四丝六忽,为仲吕之数也。
分无射四寸八分八釐四毫八丝为三分,每分一寸五分八釐七毫五丝六忽,去一分,下生仲吕,得二分,计三寸二分八釐六毫二丝三忽。在阳,倍之,六寸五分八釐三毫四丝六忽。〈在阳谓居巳也〉十二律之实第四。解曰:十二律,各得于黄钟之数也。
子,黄钟,十七万七千一百四十七 全九寸。
解曰:黄钟之数,一万九千六百八十三为一寸,积之,则九个一万九千六百八十三,为九寸。共该十七万七千一百四十七分。
半无,
一以十七万七千一百四十七之数不可分。解曰:一十七万七千一百四十七,分作两分,一分得八万八千五百七十三,两分不得均平,故不可分而无半也。
一以三分损益,上下相生之所不及,故亦无所用也。
解曰:黄钟不为他律所役,故损益不及。损益不及,故不用半。如林钟受损于黄钟三分九寸,林钟得二分六寸一分,三寸为半,非半无以成其数也。如太簇受益于林钟三分六寸,太簇得四分八寸二分,四寸为半,非半亦无以成其数也。独黄钟不然。
丑,林钟,十一万八千九十八 全六寸 半三寸不用。
解曰:凡律用半者,以上律短而下律长,或均或短不及数,故下律用半,以成宫、商、角、徵、羽之五声。林钟、南吕、应钟三律受役于黄钟,太簇为徵羽,其上太簇、姑洗、蕤宾,皆本然多寡之数,其馀为宫商角,皆依序而下,乃自为上律。而上律更无短者,而半又将何所用哉。
寅,太簇,十五万七千四百六十四 全八寸 半四
寸。
卯,南吕,十万四千九百七十六 全五寸三分 半
二寸六分,不用。
解曰:黄钟之数二千一百八十七为一分,积而三之,六千五百六十一为三分。五寸得九万八千四百一十五。合三分之数,共十万四千九百七十六。
辰,姑洗,十三万九千九百六十八 全七寸一分半三寸五分。
巳,应钟,九万三千三百一十二 全四寸六分六釐
半二寸三分三釐,不用。
解曰:黄钟之数,二百四十三为一釐,积而六之,一千四百五十八为六釐。四寸六分,得九万一千八百五十四。合六釐之数,共九万三千三百一十二。
午,蕤宾,十二万四千四百一十六 全六寸二分八釐 半三寸一分四釐。
未,大吕,十六万五千八百八十八 全八寸三分七釐六毫 半四寸一分八釐三毫。
解曰:黄钟之数,二十七为一毫,积而六之,一百六十二为六毫。八寸三分七釐,得十六万五千七百二十六。合六毫之数,共十六万五千八百八十八。
申,夷则,十一万五百九十二 全五寸五分五釐一毫 半二寸七分二釐五毫。
酉,夹钟,十四万七千四百五十六 全七寸四分三釐七毫三丝 半三寸六分六釐三毫六丝。
解曰:黄钟之数,三为一丝,积而三之为九,七寸四分三釐七毫,得十四万七千四百四十七。合二丝之数,共十四万七千四百五十六。
戌,无射,九万八千三百四 全四寸八分八釐四毫八丝 半二寸四分四釐二毫四丝。
亥,仲吕,十三万一千七十二 全六寸五分八釐三毫四丝六忽〈馀二算〉半三寸二分八釐六毫二丝三忽。
解曰:黄钟之数,一为三忽,积而六之,为二,六寸五分八釐三毫四丝,得十三万一千七十,合六忽之数,共十三万一千七十二。 数至仲吕,不生。解曰:数止于仲吕十二,不生者,何也。盖律吕相生,以三分损益。至于仲吕,寸分釐毫丝忽,虽可三分,数十三万一千七十二,并半数三分,亦不足,故不以相生也。〈二算者三忽为一也〉
寸忽可三分
二寸一分八釐七毫一丝五忽〈以三忽为丝算亦同〉
全 二寸一分八釐七毫一丝五忽〈但为一丝三忽〉
二寸一分八釐七毫一丝五忽
一寸八釐八毫七忽
半 一寸八釐八毫七忽
一寸八釐八毫七忽
数不可三分
一十三万一千七十二
四 三 六 九 一
全 四 万三 千六 百九 十 馀二
四 三 六 九
六万五千五百三十六
二 一 八 四 五一
半 二 万一 千八 百四 十五 馀一
二 一 八 四 五
变律第五。解曰:变律者,在正律之位,而非正律之声也。然律所以有变者,其故有三。其一,黄钟至尊为君,不为他律役,而每一律皆当为五声,二变共七声。如黄钟为宫,则得其正矣。其为无射之商,夷则之角,蕤宾之变徵,仲吕之徵,夹钟之羽,大吕之变宫,皆受役于他律。故皆当变。黄钟既变,其次所生之律,若仍本律,则长不成曲,亦当变焉。如黄钟为商,则太簇之角,姑洗之变徵,林钟之羽,南吕之变宫,皆随而变。如黄钟为角,则太簇之变徵,林钟之变宫,皆随其变。如为徵,则应钟为变徵。为羽,则太簇为变宫。臣之从君,理固然也。其二,以黄钟、林钟、太簇、南吕、姑洗、应钟上六律长,蕤宾、大吕、夷则、夹钟、无射、仲吕下六律短。以上律役下律,则或正或半,通而和。以下律役上律,则或正或半,戾而不和。故以上律役上律,以下律役下律,以上律役下律,皆不必变。惟以下律役上律,则必变其上律,使少短,而与下律适也。其三相生之法,至仲吕而穷,使再生六律,则上律独不能遍七声之用,下律亦无由而通。故以六三之七百二十九,因仲吕之实十三万一千七十二,三分而益之,再得六律,以为变也。其实乃仲吕之实相乘,三分益一,再生黄钟,不及旧数,止得十七万四千七百六十二。其下相因而生五律,莫不于旧为减。是皆数之自然,而非人力私智增损其间,以求合乎音韵也。其所以变有六者,以数至应钟而穷,然至此则十二律七声,循环相役以遍,莫非天然自有也。律吕之数,妙矣哉。〈其实止为律至仲律而穷不足旋宫之用〉
黄钟十七万四千七百六十二,〈小分四百八十六〉全八寸七分八釐一毫六丝二忽,不用。
半四寸三分八釐五毫三丝一忽。
解曰:仲吕之实,十三万一千七十二。以三分之,不尽二算,当有以通之。律当变者有六,故置一而六,三之得七百二十九。七百二十九因仲吕之十三万一千七十二,每仲吕之一,当七百二十九,共九千五百五十五万一千四百八十八。以三分之,每分得三千一百八十五万四百九十六。又益一分,上生黄钟,共一万二千七百四十万一千九百八十四。复以七百二十九归之,为十七万四千七百六十二个七百二十九零四百八十六,每黄钟之一,当七百二十九,为黄钟十七万四千七百六十二零三分一之二。以寸法计之,十五万七千四百六十四,得寸者八。以分法计之,一万五千三百九,得分者十。以釐法计之,一千九百四十四,得釐者八。以毫法计之,二十七,得毫者一。以丝法计之,一十八,得丝者六七百二十九。为一一小分,七百二十九为三,得三分一之二,为四百八十六,为二忽。积而计之,为十七万四千七百六十二,小分四百八十六,半四寸三分八釐五毫三丝一忽,得八万
七千三百八十一,小分二百四十三。不用全者,所受役之律,无长于此者也。下同,且黄钟君也。
林钟,十一万六千五百八〈小分三百二十四〉,
全五寸八分二釐四毫一丝一忽三初,
半二寸八分五釐六毫五丝六初。
解曰:以黄钟一万二千七百四十万一千九百八十四,三分之,每分得四千二百四十六万七千三百二十八。损一分,下生林钟,八千四百九十三万四千六百五十六。以七百二十九归之,为林钟之十一万六千五百八个七百二十九零三百二十四八十一,为一初。
太簇,十五万五千三百四十四,〈小分四百三十二〉全七寸八分二毫四丝四忽七初,不用。
半三寸八分四釐五毫六丝六忽八初。
解曰:以林钟八千四百九十三万四千六百五十六,三分之,每分得二千八百三十一万一千五百五十二。益一分,上生太簇,一万一千三百二十四万六千二百八,以七百二十九归之,为太簇之十五万五千三百四十四个七百二十九零四百二十二。
南吕,十万三千五百六十三〈小分四十五〉,
全五寸二分三釐一毫六丝一初六秒,
半二寸五分六釐七丝四忽五初二秒。
解曰:以太簇一万一千三百二十四万六千二百八,三分之,每分得三千七百七十四万八千七百三十六。损一分,下生南吕,七千五百四十九万七千四百七十二。以七百二十九归之,为南吕之十万三千五百六十三个七百二十九零四十五。
姑洗,十三万八千八十四〈小分六十〉
全七寸一釐二毫二丝一初二秒,不用。
半三寸四分五釐一毫一丝一初一秒。
解曰:以南吕七千五百四十九万七千四百七十二,三分之,每分得二千五百十六万五千八百二十四。益一分,上生姑洗,一万六十六万三千二百九十六。以七百二十九归之,为姑洗之十三万八千八十四个七百二十九零六十。
应钟,九万二千五十六〈小分四十〉,
全四寸六分七毫四丝三忽一初四秒〈馀算〉,
半二寸三分三毫六丝六忽六秒强,不用。
解曰:以姑洗一万六十六万三千二百九十六,三分之,每分得三千三百五十五万四千四百三十二。损一分,下生应钟,六千七百十万八千八百六十四。以七百二十九归之,为应钟之九万二千五百六个七百二十九零四十。
应钟六千七百十万八千八百六十四,三分之,不尽一算。
二 二 三 六 九 六 二 一
二千二百三十六万九千六百二十一〈不尽一算〉二 二 三 六 九 六 二